👇1. Q value and frequency characteristics of ceramic capacitor
⭐️The capacitance of the class Ⅰ of ceramic dielectric capacitors (such as COG) is substantially invariant with frequency over the entire usable frequency range.
Q value and resonant frequency are important indicators when high-frequency/super-frequency capacitors are used in bad resonant circuits. High-frequency/ultra-high-frequency capacitors with excellent performance have good performance in this regard, such as, COG dielectric below 10pF For ultra-high frequency ceramic capacitors with capacitance, the Q value is below 400MHz and reaches more than 1000 meters. In fact, this Q value decreases with the increase of frequency, which can be explained by the increase of loss number with frequency. When the frequency is high to a certain extent, the Q value will drop sharply (the Q value starts to drop sharply after about 6.8pF to above 1.5G), as shown in Figure 3.23, which is also consistent with the increase of ESR with the increase of frequency.
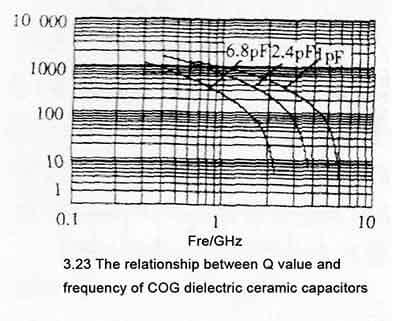
Here, “ultra-high frequency” mainly means that it can work at ultra-high frequency, and of course it can also work at various frequencies below ultra-high frequency. As can be seen from the figure, the characteristic shifts to the left as the capacitance increases. In fact, the discussion of larger capacitance will be meaningless at ultra-high frequency. For example, the 1000pF capacitive reactance is only 0.318Ω at 1GHz, while the inductance of the 1cm lead is 10nH, and the resonant frequency with the 1000pF capacitor is about 50MHz, which is 1 at 1GHz. /20, that is to say, a 1000pF capacitor is used for a resonant circuit, and its resonant frequency generally does not exceed 50MHz. At a frequency of 1MHz, it can only be used for filtering or bypassing. This is the Q value. It is meaningless.
👇2. Resonant frequency, ESR and impedance frequency characteristics
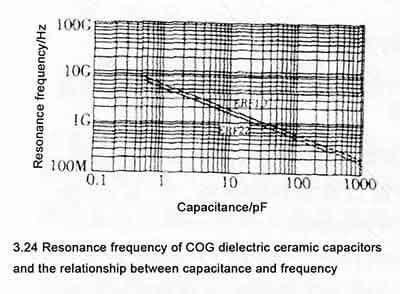
⭐️Any capacitor has its own resonance frequency, that is, the frequency at which its own capacitance and parasitic inductance form series resonance. In the same package, the parasitic inductance is basically the same. Naturally, the larger the capacitance, the lower the resonant frequency, as shown in Figure 3.24, and the smaller the package size, the higher the resonant frequency.
The ESR of the classⅠ of ceramic dielectric capacitors increases with frequency, as shown in Figure 3.24, and as the frequency decreases, the ESR characteristics gradually flatten.
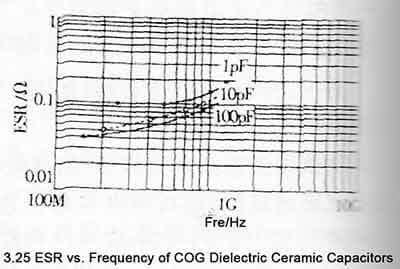
The ESR of the classⅠ of dielectric, such as COG dielectric capacitors, decreases with the increase of capacitance, as shown in Figure 3.25. The reason is obvious. As the capacitance increases, the area of the plate also increases. Under the same packaging conditions, only It can be obtained by increasing the number of layers of polar plates. Since the ESR of each layer of polar plates is basically the same, the number of parallel polar plates increases, and the ESR will inevitably decrease.
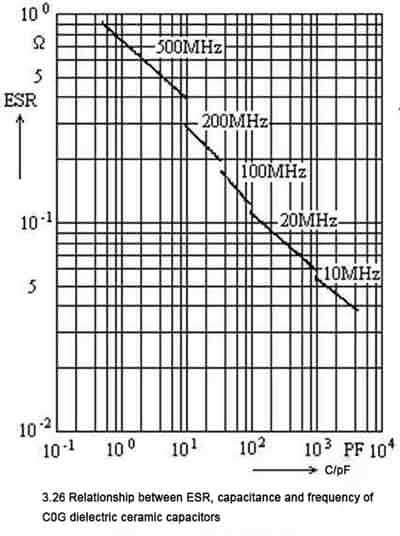
The relationship between ESR, capacitance and frequency of C0G dielectric ceramic capacitors is shown in Figure 3.26. The impedance frequency characteristics are shown in Figure 3.27.
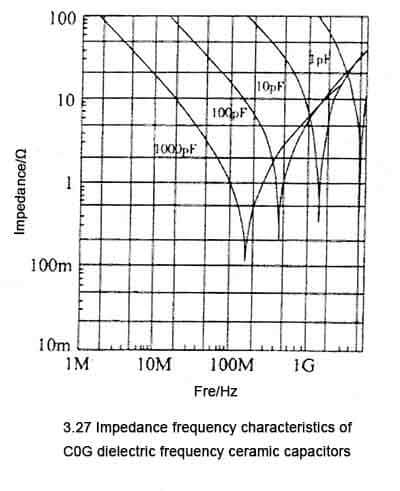
⭐️Characteristics can be divided into three parts: capacitive part, resonant part, inductive part. In the capacitive part, the capacitor exhibits capacitor characteristics, which is consistent with: Xc=(πƒ·C)-1, and the impedance decreases with the increase of frequency, as shown in the left half of the curve in Figure 3.27. In the resonance part, the inductive reactance of the parasitic inductance of the capacitor increases with the frequency to the level close to the capacitive reactance. Since the inductive reactance and the capacitive reactance are opposite in sign, the actual impedance of the capacitor in this frequency band is less than the capacitive reactance of the capacitor. When the inductive reactance is equal to When the capacitive reactance is in the resonant state, the capacitive reactance is canceled by the inductive reactance, leaving only the ESR, as shown in the characteristic curve in Figure 3.27 where the impedance drops sharply. As the frequency further increases, the inductive reactance begins to be larger than the capacitive reactance, and the capacitor begins to gradually behave as an inductive characteristic, as shown in the rising part on the right side of the characteristic curve in Figure 3.27.
The impedance frequency characteristics of the Class Ⅱ of dielectric capacitors are shown in Figure 3.28. Similar to the Class Ⅰ of dielectric capacitors, the characteristics can also be divided into three parts: capacitive part, resonant part, and inductive part. The shape of the characteristic curve is also basically the same. Different from the Class Ⅰ of dielectric capacitors, generally the capacitance of the Class Ⅱ of dielectric capacitors is much larger than that of the Class Ⅰ of capacitors, and the frequency band where the characteristic curve is located is lower than that of the Class Ⅰ of dielectric capacitors. For example, the resonance frequency of a capacitor with a capacitance of 10nF is about 50MHz, the resonance frequency of a capacitor with a capacitance of 100nF is reduced to less than 20MHz, and the resonance frequency of a capacitor with a capacitance of 10UF is reduced to 2MHz.
Similar to the Class Ⅰ capacitors, as the capacitance increases, the ESR also decreases. The difference is that the frequency characteristics of ESR have changed. Taking the 50V/10UF capacitor of X5R dielectric as an example (the right side of Figure 3.28), the ESR in the low frequency band decreases with the increase of frequency, about 100kHz, in the range of 100kHz to 1MHz. The ESR of 1MHz is reduced to the lowest value, and the ESR of the frequency band above 1MHz increases with the increase of frequency.
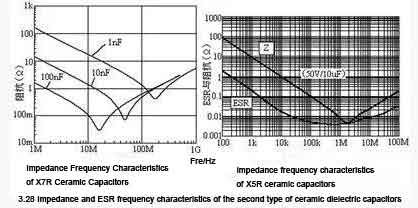
As can be seen from the figure on the right side of Figure 3.28, the ESR of the 50V/10UF Class II ceramic capacitor is only 5mΩ, which is also an extremely low ESR value among various electrical appliances.
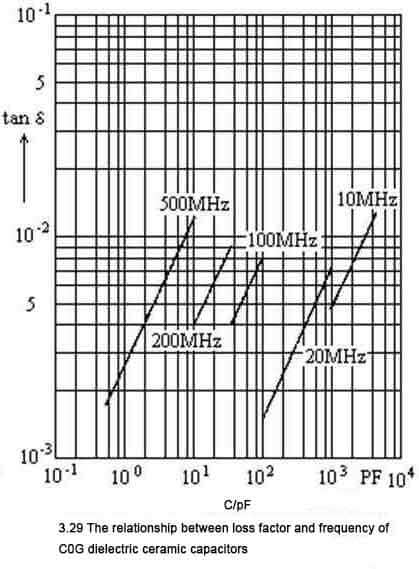
👇3. Frequency characteristics of loss factor
⭐️The relationship between loss factor and frequency: The loss factor of the Class Ⅰ of ceramic dielectric capacitor increases with the increase of frequency. The relationship between the loss factor of the Class Ⅰ of COG dielectric, capacitance and frequency is shown in Figure 3.29. Increasing the capacitive reactance decreases, so that the loss factor of the capacitor increases with the increase of the capacitance at the same frequency. The dissipation factor of capacitors of the same capacitance increases with frequency. In fact, the dielectric loss of COG media does not vary with frequency within the application frequency. The reason why the loss factor increases with frequency is that when the loss factor is measured under the condition that the terminal voltage of the capacitor is constant, as the frequency increases, the capacitor current increases, so the loss generated in the capacitor’s ESR also increases. When the frequency is higher than a certain value, the loss generated by the ESR becomes the main loss, and the loss factor at this time will increase linearly with the frequency.
⭐️The variation of the loss factor with frequency of the Class Ⅱ of ceramic dielectric capacitors is basically similar to that of the Class Ⅰ of dielectric.